Question

A sector of a circle has a central angle measure of 310 degrees. If the radius of the

circle is 2 feet, what is the area of the sector?
O 21.64 square feet
12.31 square feet
10.82 square feet
5.41 square feet​

Answer 1

`A =\pi r^2 = \pi (2ft)^2 = 4\pi`

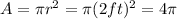
With A the entire area of the circle

`A_s = (\pi)/(360) \pi r^2`

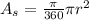
Since the area of a sector is a fraction of the entire area. Replacing the info given we got:

`A_s = (310)/(360) 4\pi = 10.82 ft^2`

And then the best option for this case would be:

10.82 square feet

Explanation:

For this case we know the radius of the circle
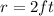`r = 2ft` and the area of the circle would be given by:

`A =\pi r^2 = \pi (2ft)^2 = 4\pi`

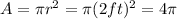
We also know that we have a sector with a central angle of 310 degrees and the area for this sector would be given by:

`A_s = (\pi)/(360) \pi r^2`

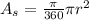
Since the area of a sector is a fraction of the entire area. Replacing the info given we got:

`A_s = (310)/(360) 4\pi = 10.82 ft^2`

And then the best option for this case would be:

10.82 square feet