Answer:
2 inches
Explanation:
The most important thing to note when approaching this question is that we are dealing with similar triangles.
Similar triangles are triangles that have the same angles to each other, but different side lengths. Here our similar triangles are the main big one and the smaller one contained inside. We know they're similar because they both have a right angle, and they both share the angle at the top (there is no need to prove all 3 angles are shared, if 2 angles are shared the 3rd angle must be equal since all angles in a triangle add to a fixed number, 180).
The corresponding sides of similar triangles are in ratio to each other, so the ratio of the bottom sides, 6 and 9, will be the same as the ratio of the left-hand sides, x and (x+4). Write these ratio as fractions equal to one another:
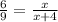
Cross multiply:
6(x+4)=9(4)
6x+24=36
6x=12
x=2