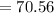Answer:
The correct answer to the following question will be "70.56".
Explanation:
The given values are:
Loan requires, PV = $100,000
Years = 20
Number of months, n = 240
Rate interest = 4.90000%
Monthly rate, r = 0.408333%
Monthly rental payment = $725
As we know,
![PV=PMT* ((1)/(r))* [1-[(1)/((1+r)^n)]]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/ugarvew9m077lqes4vta10mjls349ey8ev.png)
On putting the values in the above formula, we get
⇒
![100000=PMT* ((1)/(0.004083333))* [1-((1)/((1+0.004083333^(240))))]](https://img.qammunity.org/2021/formulas/mathematics/middle-school/ulbxb8zdlvkb8vmjfs7dr1u1luouyf79v9.png)
⇒
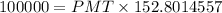
⇒
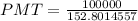
⇒

Now,
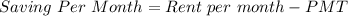
On putting the values, we get
⇒

⇒