Question

Identifying trig ratios :in STU ,the measure of U= 90° , SU=7 , UT=24, and TS=25, what ratio represents the tangent of T

Answer 1

The ratio representing the tangent of T is 7 : 24.

Explanation:

Consider the right angles triangle STU below.

In the triangle STU, the angle U is 90°.

The measure of the sides are as as follows:

Perpendicular = SU = 7 units

Base = UT = 24 units

Hypotenuse = TS = 25 units.

According to the Pythagorean theorem,

Hypotenuse² = Perpendicular² + Base²

Check if the above measurements satisfies the theorem or not.

Hypotenuse² = Perpendicular² + Base²

(25)² = (24)² + (7)²

625 = 576 + 49

625 = 625

Thus, the measurements are correct.

Now according to the trigonometric identities for a right angles triangle, the tangent of an angle is:

`tan\ \theta=(Perpendicular)/(Base)`

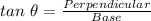
Compute the tangent of angle T as follows:

`tan\ \text{T}=(SU)/(UT)`

`tan\ \text{T}=(7)/(24)`

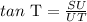
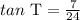
Thus, the ratio representing the tangent of T is 7 : 24.