Question

A system initially has an internal energy E of 501 J. It undergoes a process during which it releases 111 J of heat energy to the surroundings, and does work of 222 J. What is the final energy of the system, in J?

Answer 1

The final energy of the system is 168 J

Step-by-step explanation:

`\triangle Q = \triangle U + W`

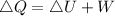
Heat energy released to the surroundings,
`\triangle Q = -111 J`

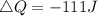
Work done, W = 222 J

`-111 = \triangle U + 222\\ \triangle U = -111 - 222\\\triangle U = - 333 J`

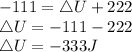
The initial internal energy,
`E_(1) = 501 J`

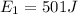
The change in internal energy is given by the formula,
`\triangle U = E_(2) - E_(1)`

`E_(2) = \triangle U + E_(1)\\E_(2) = -333 + 501\\E_(2) = 168 J`

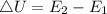
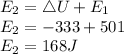
The final energy of the system is 168 J