Answer:
Perimeter of given regular hexagon is 48.5 ft.
Explanation:
Let ABCDEF be the regular hexagon as shown in the attached figure.
O be the intersection point of the diagonals EB, FC and AD.
As per the property of regular hexagon, all the 6 triangles formed are equilateral triangles.
In other words,
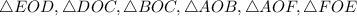 are equilateral
are equilateral
 .
.
Area of an equilateral
 is defined as :
is defined as :
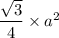
Where a is the side of
 .
.
Area of hexagon =

We are given that area of hexagon = 169.74
Let s be the side of hexagon.
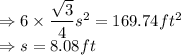
A regular Hexagon is made up of 6 equal sides, so
Perimeter of a regular hexagon =

Perimeter =

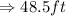
So, perimeter of given regular hexagon is
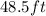 .
.