Question

If PbI2(s) is dissolved in 1.0MNaI(aq) , is the maximum possible concentration of Pb2+(aq) in the solution greater than, less than, or equal to the concentration of Pb2+(aq) in the solution in part ( a ) ? Explain.

Answer 1

`\mathbf{s =\sqrt [3]{(K_(sp))/(4)}}`

Less than the concentration of Pb2+(aq) in the solution in part ( a )

Step-by-step explanation:

From the question:

A)

We assume that s to be the solubility of PbI₂.

The equation of the reaction is given as :

PbI₂(s) ⇌ Pb²⁺(aq) + 2I⁻(aq); Ksp = 7 × 10⁻⁹

[Pb²⁺] = s

Then [I⁻] = 2s

`K_(sp) =\text{[Pb$^(2+)$][I$^(-)$]}^(2) = s* (2s)^(2) = 4s^(3)\\s^(3) = (K_(sp))/(4)\\\\s =\mathbf{ \sqrt [3]{(K_(sp))/(4)}}\\\\\text{The mathematical expressionthat can be used to determine the value of }\mathbf{s =\sqrt [3]{(K_(sp))/(4)}}`

B)

The Concentration of Pb²⁺ in water is calculated as :

`\mathbf{s =\sqrt [3]{(K_(sp))/(4)}}`

`\mathbf{s =\sqrt [3]{(7*10^(-9))/(4)}}`

`\mathbf{s} =\sqrt[3]{1.75*10^(-9)}`

`\mathbf{s} =\mathbf{1.21*10^(-3) \ mol/L }`

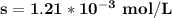
The Concentration of Pb²⁺ in 1.0 mol·L⁻¹ NaI

`\mathbf{PbCl{_2}} \leftrightharpoons \ \ \ \ \ \ \ \mathbf{Pb^(2+)} \ \ \ \ \ + \ \ \ \ \ \ \ \mathbf{2 I^-}`

`\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf0} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{1.0}`

`\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{+x} \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{+2x}`

`\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{+x} \ \ \ \ \ \ \ \ \ \ \ \ \mathbf{1.0+2x}`

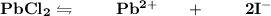
The equilibrium constant:

`K_(sp) =[Pb^(2+)}][I^-]^2 \\ \\ K_(sp) = s*(1.0*2s)^2 =7*1.0^(-9) \\ \\ s = 7*10^(-9) \ \ m/L`

It is now clear that maximum possible concentration of Pb²⁺ in the solution is less than that in the solution in part (A). This happens due to the common ion effect. The added iodide ion forces the position of equilibrium to shift to the left, reducing the concentration of Pb²⁺.