Given Information:
Initial temperature of aluminum block = 26.5°C
Heat flux = 4000 w/m²
Time = 2112 seconds
Time = 30 minutes = 30*60 = 1800 seconds
Required Information:
Rise in surface temperature = ?
Answer:
Rise in surface temperature = 8.6 °C after 2112 seconds
Rise in surface temperature = 8 °C after 30 minutes
Step-by-step explanation:
The surface temperature of the aluminum block is given by
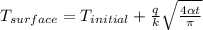
Where q is the heat flux supplied to aluminum block, k is the conductivity of pure aluminum and α is the diffusivity of pure aluminum.
After t = 2112 sec:
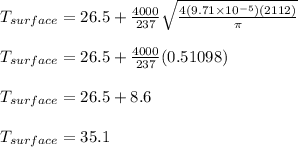
The rise in the surface temperature is
Rise = 35.1 - 26.5 = 8.6 °C
Therefore, the surface temperature of the block will rise by 8.6 °C after 2112 seconds.
After t = 30 mins:
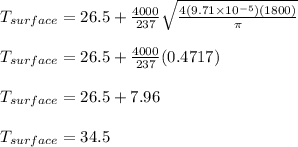
The rise in the surface temperature is
Rise = 34.5 - 26.5 = 8 °C
Therefore, the surface temperature of the block will rise by 8 °C after 30 minutes.