Answer:
C.
 ft
ft
Explanation:
Given
The length of one side of the triangle = 3 ft
Required
The perimeter
Given that the perimeter is an isosceles right triangle, this means that two sides (the opposite and adjacent) are actually equal while the hypothenus is longer.
So, we can easily assume that
Opposite = 3 ft
Adjacent = 3 ft
then we solve for the hypothenus of the triangle
Using Pythagoras theorem
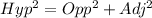
Substitute 3 for opposite and adjacent
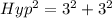

Take square root of both sides
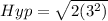
Split the surd
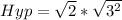
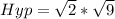
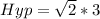

Now that we have the three sides of the triangle, the perimeter is calculated by adding the values of the three sides
Perimeter = Opposite + Adjacent + Hypothenus
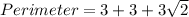

Hence, the perimeter of the triangle is
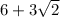 ft
ft