Question

The average cost of tuition and room and board at a small private liberal arts college is reported to be $8,500 per term, but a financial administrator believes that the average cost is higher. A study conducted using 350 small liberal arts colleges showed that the average cost per term is $8,745. The population standard deviation is $1,200. Let ? = 0.05. What is the test statistic for this test?

A. ±3.82

B. +0.204

C. -3.82

D. +3.82

Answer 1

D) + 3.82

Z- test statistic value = 3.819≅ 3.82

Explanation:

Explanation:-

Given data the sample size 'n' = 350

Population mean 'μ' = $8,500

Sample mean 'x⁻' = $8,500

The population standard deviation is 'σ' = $1,200

The level of significance ∝ =0.05

The tabulated value Z₀.₉₅ = 1.96

Null hypothesis: There is no significant difference between the small private liberal arts college and the financial administrator.

x⁻= μ

Alternative hypothesis: x⁻> μ

Test statistic

`Z = (x^(-) -mean )/((S.D)/(√(n) ) )`

`Z = (8745-8500)/((1200)/(√(350) ) )`

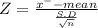
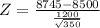
On calculation , we get

`Z = (245)/(64.14) = 3.819`

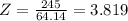
Z- test statistic value = 3.819≅ 3.82

Conclusion:-

The calculated value = 3.82 > 1.96 at 0.05 level of significance.

The null hypothesis is rejected

Alternative hypothesis is accepted

The financial administrator believes that the average cost is higher than the small private liberal arts college