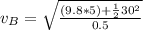Complete Question
The complete question is shown on the first uploaded image
Answer:
The velocity of the bus at B is
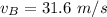
Step-by-step explanation:
Let's take position B as base point .
From the diagram height between point B and A ia mathematically evaluated as
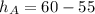
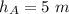
From the question we are told that
The velocity at location A is
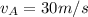
According the law of conservation of energy
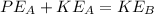
Where
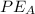 is the potential energy at A which is mathematically represented as
is the potential energy at A which is mathematically represented as
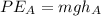
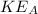 is the kinetic energy energy at A which is mathematically represented as
is the kinetic energy energy at A which is mathematically represented as
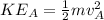
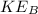 is the kinetic energy at A which is mathematically represented as
is the kinetic energy at A which is mathematically represented as
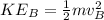
Where
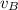 is the velocity at location B
is the velocity at location B
So
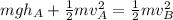
Making
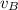 the subject of the formula
the subject of the formula
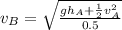
Substituting values