Answer:
Daniel's equation will have a vertical translation by 2 units in the positive direction.
Explanation:
Errol's bike ride can be modeled by the equation,

Slope of the equation =
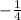
Here slope defines the rate of change of distance from Errol's house.
Y-intercept = 2, which represents the distance of the school from his home.
Let the equation that represents the equation is,
d(t) = mt + b
Errol's friend Daniel lives 4 miles away from school that means y intercept of the equation (b) = 4
Since Daniel drives his bike at the same pace as Errol, slope will be same.
Equation that models the distance will be

If we compare both the equations, slopes are same but y-intercepts have a difference of 2 units
Therefore, the graph from the Daniel's equation will have a vertical translation by 2 units in the positive direction.