Question

The energy levels of a quantum harmonic oscillator are given by En = n + 1 2 ¯h ω where 2π ¯h = h and h is Planck’s Constant. The energy of a quantum of electromagnetic radiation (a photon) is Eλ = h c λ where λ is the wavelength of the radiation and c is the speed of light. If a harmonic oscillator transitions down one energy level, what is the wavelength of electromagnetic radiation emitted?

Answer 1

2πc/w

Step-by-step explanation:

To find the wavelength you take into account the difference in energy of two adjacent states n+1 and n:

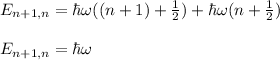`E_(n+1,n)=\hbar \omega((n+1)+(1)/(2))+\hbar \omega(n+(1)/(2))\\\\E_(n+1,n)=\hbar \omega`(1)

hbar = h/2π

this energy is also the energy of an emitted photon in the transition, that is:

`E_(\lambda)=h(c)/(\lambda)` (2)

you equal the equations (1) and (2) and compute the wavelength:

`E_(\lambda)=E_(n+1,n)\\\\h(c)/(\lambda)=(h)/(2\pi)\omega\\\\\lambda=(2\pi c)/(\omega)`

hence, the wavelength of the emitted photon is 2πc/w