Question

According to a survey of 500, the mean income before taxes of consumer units (i.e., households) inthe U.S. was $60,533 with a standard error of 717.51. Find the margin of error for constructing a95% confidence interval on the population mean income before taxes of all consumer units in theU.S

Answer 1

The margin of error for constructing a 95% confidence interval on the population mean income before taxes of all consumer units in the U.S is 1406.32.

Explanation:

We are given that according to a survey of 500, the mean income before taxes of consumer units (i.e., households) in the U.S. was $60,533 with a standard error of 717.51.

Margin of error tells us that how much our sample mean value deviates from the true population value.

Margin of error is calculated using the following formula;

Margin of error =
`Z_(_(\alpha)/(2)_) * \text{Standard of Error}`

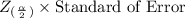
where,
`\alpha` = level of significance = 1 - confidence level

= 1 - 0.95 = 0.05 or 5%

Standard of Error =
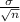`(\sigma)/(√(n) )` = 717.51

Now, the value of z at 2.5% level of significance (
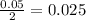`(0.05)/(2) =0.025`) is given in the z table as 1.96, that means;

Margin of error =
`Z_(_(\alpha)/(2)_) * \text{Standard of Error}`

=
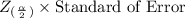
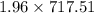`1.96 * 717.51` = 1406.32

Hence, the margin of error for constructing a 95% confidence interval on the population mean income before taxes of all consumer units in the U.S is 1406.32.