Question

a square red rug has a purple square in the center. the side length of the purple square is x inches. the width of the red band that surrounds the purple square is 5 in. what is the area of the red band

Answer 1

Area of red band is
`(20x + 100) inch^(2)`

Explanation:

We know that area of square =
`side^(2)`

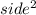
Please refer to the attached figure, we have to calculate the area of red band.

Required area = Area of square ABCD - Area of purple square

Side of purple square =
`x`

So, area of purple square =
`x^(2)`

ABCD is a square with purple square at the center and there is symmetry in the figure.

So, width of red band towards both the end is 5 inches.

`\Rightarrow \text{side of }ABCD = 5 + 5 +x = (x+10) inches`

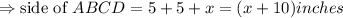
Required area =
`(x+10)^(2) - x^(2)`

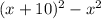
Using formula
`a^(2) - b^(2) = (a-b)* (a+b)`

`\Rightarrow (x+10-x)(x+10+x)\\\Rightarrow (10)(2x+10)\\\Rightarrow (20x+100)`

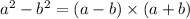
Hence, Area of red band is
`(20x + 100) inch^(2)`