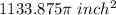Answer:
volume of metal =
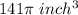
Surface area of cylinder to be powder-coated=
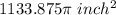
Explanation:
Radius of outer circle, R = 6 inch
Radius of inner circle, r = 5.75 inch
Height of cylinder, h = 4 ft = 4 * 12 inch = 48 inch
Calculating the volume of metal used to build this pipe:
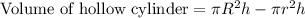
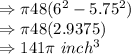
Inner and outer surfaces are to be powder-coated.
Total surface area = Lateral surface area + Area of solid bases
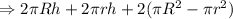
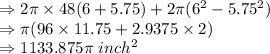
So, volume of metal =
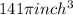
Surface area of cylinder to be powder-coated=