Question

In circle C, m = 148°, m = 86°, and m∠EPF = 116°. What is the measure of arc FG?

Answer 1

106 degrees is correct.

Explanation:

I just tested it in Plato and got a 100%

Answer 2

The measure of the arc FG is 106°.

Explanation:

Givens.

Arc CD is 86°.

Angle EPF is 116°.

Arc CG is 148°.

`\angle EPF + \angle FPD = 180\°\\116\°+ \angle FPD = 180\°\\\angle FPD = 180\° - 116\°\\\angle FPD = 64\°` By supplementary angles, and basic algebra.

`\angle FPD = (1)/(2)(m(CG)-m(DF) )`

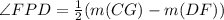
Solving for arc DF

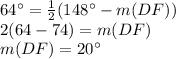`64\° =(1)/(2)(148\° - m(DF)) \\2(64-74)=m(DF)\\m(DF)=20\°`, by the theorem of the external angle formed by two secants.

Now, we know that the total arc lenght of a circle is 360°, so

`m(CD)+m(CG)+m(FG)+m(DF)=360\°\\86+148+m(FG)+20=360\\m(FG)=360-254\\m(FG)=106\°`

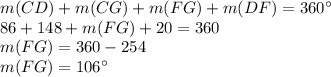
Therefore, the measure of the arc FG is 106°.