Answer:
For this case we know that the confidence level is 90% so then the significance level is
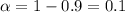 and
and
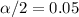 . And we can find in the normal standard distribution a value who accumulates 0.5 of the area on each tail and we got:
. And we can find in the normal standard distribution a value who accumulates 0.5 of the area on each tail and we got:
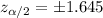
And the best option would be:
1.645
Explanation:
We assume that the parameter of interest is
 and we can assume that the distribution for this parameter is normally distributed so then the confidence interval assuming a two sided interval is given by:
and we can assume that the distribution for this parameter is normally distributed so then the confidence interval assuming a two sided interval is given by:
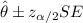
Where
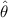 represent the estimator for the parameter, SE the standard error and
represent the estimator for the parameter, SE the standard error and
 the critical value.
the critical value.
For this case we know that the confidence level is 90% so then the significance level is
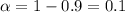 and
and
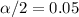 . And we can find in the normal standard distribution a value who accumulates 0.5 of the area on each tail and we got:
. And we can find in the normal standard distribution a value who accumulates 0.5 of the area on each tail and we got:
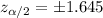
And the best option would be:
1.645