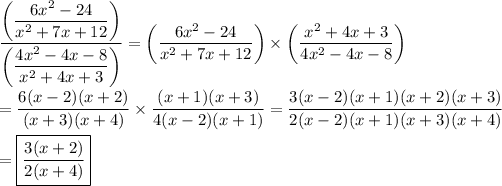Answer:
3(x+2)/(2(x+4))
Explanation:
A compound fraction is simplified by rewriting it as a simple fraction, and reducing it to lowest terms by cancelling common factors from numerator and denominator. The division of one fraction by another is accomplished in the usual way: multiply the numerator by the inverse of the denominator.
__