Question

Jay has a 20 foot ladder that he leaned against the outside wall of his house. Jay put the base of the ladder 4 feet away from the house. How far up the wall of the house is the top of the ladder? Sketch on your graph paper. (Hint) It would be a right triangle. Then, use the quadratic formula to solve.

Answer 1

The top of the ladder is 19.6 ft up the wall.

Explanation:

We have a 20-ft ladder leaned against a wall. The distance from the wall to the base of the ladder is 4 ft.

We have to calculate how far up the wall of the house is the top of the ladder.

To calculate this we use the Pithagorean theorem, where:

`L^2=b^2+h^2`

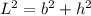
L: length of the ladder (20 ft), b: distance between the base of the ladder and the wall (4 ft) and h: height of the ladder (x, to calculate). See figure attached.

Then we can write:

`20^2=4^2+x^2\\\\x^2=20^2-4^2=400-16=384\\\\x=√(384)\approx 19.6`

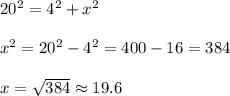
The top of the ladder is 19.6 ft up the wall.

Answer 2

19.6ft

Explanation:

The set up will be a right angled triangle as shown in the attachment.

The length of the ladder will be the hypotenuse of the triangle,

The base of the ladder which is 4feet aaway from the house will be the adjacent side

The height of the wall will be the opposite side.

According to Pythagoras theorem

Hypotenuse² = opposite²+ adjacent²

Given Hypotenuse = 20ft

Adjacent = 4ft

Height = ?

20² = opp² + 4²

Opposite² = 20²-4²

Opposite² = 400-16

Opposite = √384

Opposite = 19.6ft

The ladder was 19.6ft up the wall