Answer:
1. See below
2. F(x) = -0.10x² + 8x + 200
3. You earn the maximum income of S/320
4. The income decreases
5. x < 0; x > 100
Explanation:
1. Strategies
Let x = the days
Then 100 - x = the kilograms of oranges each day
and 0.10x = the daily price increase
and 2 + 0.10x = the daily price
Income = (kilograms of oranges) × (price per kilogram)
F(x)= (100 - x)(2 + 0.10x)
2. Another expression for F(x)
You could multiply the factors to get a polynomial in its standard form.
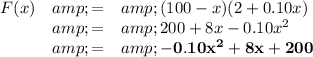
3. If sales are made in 20 da

4. If sales are made after 40 da
(a) If sales are made on Day 40
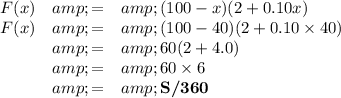
(b) If sales are made on Day 41
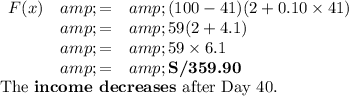
5. Unuseful parts of the graph
(a) x <0
We can't have negative times because we received the oranges for sale only on Day 0.
(b) x > 100
1 kg of oranges is damaged each day.
After 100 da, there are no more oranges to sell.
The parts of the graph below x = 0 and above x = 100 do not contribute to resolution of the problem.