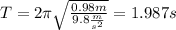Answer:
1)
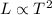
Using the condition given:

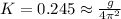
So then if we want to create an equation we need to do this:
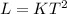
With K a constant. For this case the period of a pendulumn is given by this general expression:
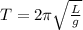
Where L is the length in m and g the gravity
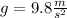 .
.
2)
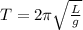
If we square both sides of the equation we got:
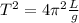
And solving for L we got:

Replacing we got:

3)
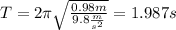
Explanation:
Part 1
For this case we know the following info: The length, l cm, of a simple pendulum is directly proportional to the square of its period (time taken to complete one oscillation), T seconds.
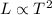
Using the condition given:

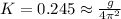
So then if we want to create an equation we need to do this:
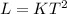
With K a constant. For this case the period of a pendulumn is given by this general expression:
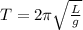
Where L is the length in m and g the gravity
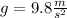 .
.
Part 2
For this case using the function in part a we got:
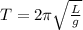
If we square both sides of the equation we got:
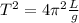
And solving for L we got:

Replacing we got:

Part 3
For this case using the function in part a we got:
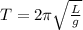
Replacing we got: