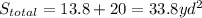Answer:
The slant height of the pyramid refers to the height of one face-triangle. Now, the cube has dimensions of 2 x 2 x 2, which means the height, base and length of the pyramid are equal, that's why is a squared pyramid.
Notice that the slant height forms a right triangle with two faces of the cube, and the pyramid intercepts the cube at the middlepoint of the plane.
First, we need to find the half-length of a diagonal, which is a leg of the right triangle formed by the slant height.
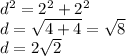
The part related with the slant height is
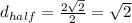
So, the slant height is
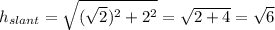
Therefore, the slant height is the square root of 6 yards.
The surface area of a squared pyramid is
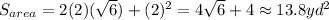
The five faces of the cube have a surface area
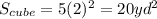
Therefore, the composite surface area of the figure is