Answer:
a)
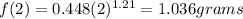
b)
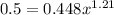
Dividing both sides by 0.448 we got:
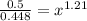
We can appy the exponent
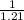 in both sides of the equation and we got:
in both sides of the equation and we got:

Explanation:
For this case we know the following function:
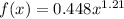
The notation is: x is the weight of the crab in grams, and the output f(x) is the weight of the claws in grams.
Part a
For this case we just need to replace x = 2 gram in the function and we got:
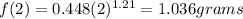
Part b
For this case we know tha value for
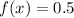 and we want to find the value of x who satisfy this condition:
and we want to find the value of x who satisfy this condition:
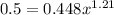
Dividing both sides by 0.448 we got:
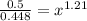
We can appy the exponent
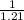 in both sides of the equation and we got:
in both sides of the equation and we got:
