Question

The lifespans of tigers in a particular zoo are

normally distributed. The average tiger lives 22.4

years; the standard deviation is 2.7 years.

Use the empirical rule (68 – 95 – 99.7%) to

estimate the probability of a tiger living less

than 14.3 years.

Answer 1

0.15%

Explanation:

Answer 2

`z = (14.3-22.4)/(2.7)=-3`

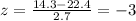
Since we know that 99.7% of the data are between 3 deviations from the mean we can conclude that:

`P(X <14.3)= (1-0.997)/(2)= 0.0015`

Since we know that the normal distribution is symmetric for this reason we divide by 2

Explanation:

For this case we know that the lifespans of tigers X are normally distributed:

`X \sim N (\mu = 22.4 , \sigma =2.7)`

From the empirical rule we know that we have 68% of the values within one deviation from the mean, 95% within 2 deviations and 99.7% within 3 deviations.

We want to find this probability:

`P(X<14.3)`

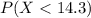
And we can use the z score formula given by:

`z = (X -\mu)/(\sigma)`

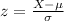
In order to find how many deviations above/below we are from the mean. And if we find the z score for 14.3 we got:

`z = (14.3-22.4)/(2.7)=-3`

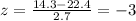
Since we know that 99.7% of the data are between 3 deviations from the mean we can conclude that:

`P(X <14.3 )= (1-0.997)/(2)= 0.0015`

Since we know that the normal distribution is symmetric for this reason we divide by 2