Question

The length of the arc intercepted by a central angle of 3/9 pie is 3.6 feet long. How long is the radius of the circle?

A)2.33feet

B)3.44 feet

C)6.88 feet

D)3.77 feet

Answer 1

B) 3.44 feet

The Radius of the circle 'r' = 3.439 ≅3.44 feet

Explanation

Step(i):-

Given data the length of arc = 3.6 feet long

l = 3.6 feet

Given central angle 'θ' =
`(3)/(9) \pi`

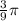
Step(ii):-

The arc length 'l' of a circle of radius 'r' with central angle 'θ' radians is given by

Arc length l = r θ

3.6 = r (
`(3)/(9) \pi`)

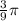put π = 3.14

now simplification, we get

`r = (3.6 X9)/(3\pi )`

`r = (3.6 X9)/(3X3.14 ) = (32.4)/(9.42) = 3.439`

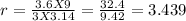
Conclusion:-

The Radius of the circle 'r' = 3.439 ≅3.44 feet