Question

g The ENGR/PHYS 216 faculty have a final exam grade distribution that is, miraculously, exactly a normal distribution. Last year, the final exam average was 78 with a standard deviation of 8 points. What is the minimum score you have to make on the final exam to be in the top 10% of students and guarantee yourself an A? Round your answer to 1 decimal place for entry into eCampus. Do not enter units. Example: 12.3

Answer 1

The minimum score you have to make on the final exam to be in the top 10% of students and guarantee yourself an A is 88.3 points.

Explanation:

We are given that the ENGR/PHYS 216 faculty have a final exam grade distribution that is, miraculously, exactly a normal distribution.

Last year, the final exam average was 78 with a standard deviation of 8 points.

Let X = final exam grade distribution

SO, X ~ Normal(
`\mu=78,\sigma^(2) =8^(2)`)

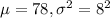The z score probability distribution for normal distribution is given by;

Z =
`(X-\mu)/(\sigma)` ~ N(0,1)

where,
`\mu` = population mean = 78 points

`\sigma` = standard deviation = 8 points

Now, the minimum score we have to make on the final exam to be in the top 10% of students and guarantee yourself an A is given by;

P(X > x) = 0.10 {where x is required minimum score}

P(
`(X-\mu)/(\sigma)` >
`(x-78)/(8)` ) = 0.10

P(Z >
`(x-78)/(8)` ) = 0.10

Now, in the z table the critical value of X which represents the top 10% of the probability area is given as 1.282, that means;

`(x-78)/(8)` = 1.282

x - 78 =
`1.282 * 8`

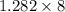
x = 78 + 10.26 = 88.3 points

Hence, the minimum score you have to make on the final exam to be in the top 10% of students and guarantee yourself an A is 88.3 points.