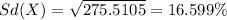Answer:
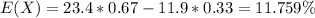
Now we can find the second central moment with this formula:
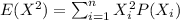
And replacing we got:
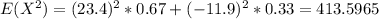
And the variance is given by:
![Var(X) = E(X^2) - [E(X)]^2](https://img.qammunity.org/2021/formulas/mathematics/college/fb2daxn97pbuqqw9lk3576dsvozhc3gnaz.png)
And replacing we got:
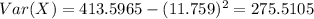
And finally the deviation would be:
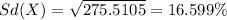
Explanation:
We can define the random variable of interest X as the return from a stock and we know the following conditions:
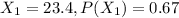 represent the result if the economy improves
represent the result if the economy improves
 represent the result if we have a recession
represent the result if we have a recession
We want to find the standard deviation for the returns on the stock. We need to begin finding the mean with this formula:
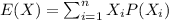
And replacing the data given we got:
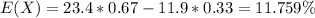
Now we can find the second central moment with this formula:
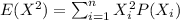
And replacing we got:
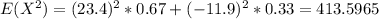
And the variance is given by:
![Var(X) = E(X^2) - [E(X)]^2](https://img.qammunity.org/2021/formulas/mathematics/college/fb2daxn97pbuqqw9lk3576dsvozhc3gnaz.png)
And replacing we got:
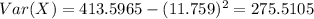
And finally the deviation would be: