Question

In a random survey of 500 doctors that practice specialized medicine, 20% felt that the government should control health care. In a random sample of 800 doctors that were general practitioners, 30% felt that the government should control health care. Test the claim that there is a difference in the proportions. Use a = 0.10

Answer 1

The calculated value Z = 3.99

The calculated value Z = 3.99 > 1.645 at 10% level of significance

Alternative hypothesis is Accepted

There is a difference between in the given two proportions.

Explanation:

Step(i):-

Given data random survey of 500 doctors that practice specialized medicine.

First sample size 'n₁' = 500

Given data 20% felt that the government should control health care.

The first sample proportion p₁ = 20% =0.20

Given data a random sample of 800 doctors that were general practitioners

second sample size 'n₂' = 800

given data 30% felt that the government should control health care

The second sample proportion p₂ = 30% =0.30

Step(ii):-

Null hypothesis:- H₀: There is no significant difference between the Proportions.

Alternative hypothesis:- H₁: There is significant difference between the Proportions.

Test statistic

`Z = \frac{p_(1)-p_(2) }{\sqrt{PQ((1)/(n_(1) ) }+(1)/(n_(2) ) ) }`

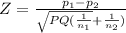
Where P

`P = (n_(1)p_(1) + n_(2) p_(2) )/(n_(1) + n_(2) )`

`P = (500X0.20 + 800X0.30 )/(500+800 )`

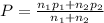
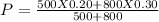
P = 0.2615

Q = 1-P = 1- 0.2615 = 0.7385

Now

Test statistic

`Z = \frac{0.20-0.30 }{\sqrt{(0.2615X0.7385)((1)/(500) }+(1)/(800 ) ) }`

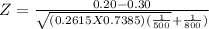
On calculation we get

`Z = (-0.10)/(√(0.000627) )`

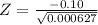
|Z| = | -3.99|

The calculated value Z = 3.99

The tabulated value

`Z(\alpha )/(2) = Z(0.10)/(2) = Z_(0.05) = 1.645`

Conclusion:-

The calculated value Z = 3.99 > 1.645 at 10% level of significance

Null hypothesis is rejected

Alternative hypothesis is Accepted

There is a difference between in the given two proportions.