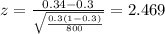Answer:
A political strategist wants to test the claim that the percentage of residents who favor construction is more than 30%, so then that represent our claim and needs to be on the alternative hypothesis.
Based on this the correct system of hypothesis are:
Null hypothesis:
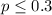
Alternative hypothesis

Explanation:
We have the following info given from the problem:
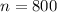 the random sample of voters selected from the town
the random sample of voters selected from the town
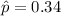 represent the proportion of residents favored construction
represent the proportion of residents favored construction
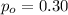 represent the value desired to test.
represent the value desired to test.
A political strategist wants to test the claim that the percentage of residents who favor construction is more than 30%, so then that represent our claim and needs to be on the alternative hypothesis.
Based on this the correct system of hypothesis are:
Null hypothesis:
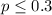
Alternative hypothesis

And in order to test this hypothesis we can use a one sample z test for a population proportion and the statistic would be given by:
 (1)
(1)
And with the data given we have: