Question

The mean per capita income is 20,90820,908 dollars per annum with a standard deviation of 407407 dollars per annum. What is the probability that the sample mean would differ from the true mean by less than 2828 dollars if a sample of 5555 persons is randomly selected? Round your answer to four decimal places.

Answer 1

`z=(20880-20908)/((407)/(√(55)))= -0.51`

`z=(20936-20908)/((407)/(√(55)))= 0.51`

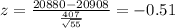
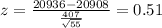
Then we can find the probability of interest with this difference:

`P(-0.51<z<0.51)=P(z<0.51)-P(z<-0.51)`

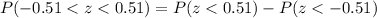
And using the normal standard distribution or excel we got:

`P(-0.51<z<0.51)=P(z<0.51)-P(z<-0.51)=0.6950 -0.3050= 0.390`

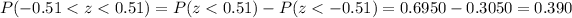
So then the probability that the sample mean would differ from the true mean by less than 28 dollars from the sample of 55 is approximately 0.390

Explanation:

We define the variable of interest as the per capita income and we know the following properties for this variable:

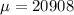`\mu=20908` and
`\sigma=407`

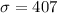
We want to find this probability:

`P(20908-28<\bar X<20908+28) = P(20880< \bar X< 20936)`

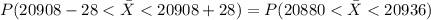
We select a sample size of n=55 and we define the z score formula given by:

`z=(x-\mu)/((\sigma)/(√(n)))`

We can find the z score then for 20880 and 20936 and we got:

`z=(20880-20908)/((407)/(√(55)))= -0.51`

`z=(20936-20908)/((407)/(√(55)))= 0.51`

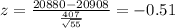
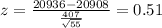
Then we can find the probability of interest with this difference:

`P(-0.51<z<0.51)=P(z<0.51)-P(z<-0.51)`

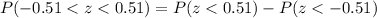
And using the normal standard distribution or excel we got:

`P(-0.51<z<0.51)=P(z<0.51)-P(z<-0.51)=0.6950 -0.3050= 0.390`

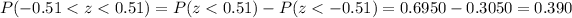
So then the probability that the sample mean would differ from the true mean by less than 28 dollars from the sample of 55 is approximately 0.390