Answer:
Step-by-step explanation:
Let the required velocity of rocket be v .
We shall use the formula of time dilation to find the velocity of rocket .
t =
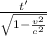
t = 430
t' = 38
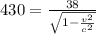

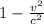 = .0078
= .0078
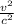 =.9922
=.9922
 = .996
= .996
v = .996 x 3 x 10⁸ m /s
= 2.988 x 10⁸ m /s
B )
Kinetic energy of rocket
= 1/2 m v²
= .5 x 20000 x (2.988 x 10⁸ )²
= 8.9 x 10²⁰ J .
C )
This energy is 8.9 times the energy requirement of United states in the year 2005 .