Answer:
a) For this case the best point estimate of the population mean weight loss of all overweight adults who follow the Atkins program is the sample mean:
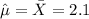
b)
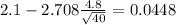
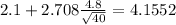
c) Since the confidence interval contains only positive values we can conclude that the program is effective and is enough evidence at 1% of significance to conclude that the true weigth loss is higher than 0.
Explanation:
Data given
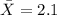 represent the sample mean for the weigth loss
represent the sample mean for the weigth loss
 population mean
population mean
s=4.8 represent the sample standard deviation
n=40 represent the sample size
Part a
For this case the best point estimate of the population mean weight loss of all overweight adults who follow the Atkins program is the sample mean:
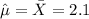
Part b
The confidence interval for the true mean is given by the following formula:
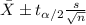 (1)
(1)
The degrees of freedom are given by:
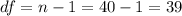
The Confidence level is 0.99 or 99%, the significance is
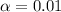 and
and
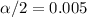 , the critical value for this case is
, the critical value for this case is
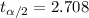
The confidence interval is given by:
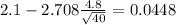
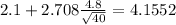
Part c
Since the confidence interval contains only positive values we can conclude that the program is effective and is enough evidence at 1% of significance to conclude that the true weigth loss is higher than 0.