Question

The profit that the vendor makes per day by selling x pretzels is given by the function P(x) = - 4x +2,400x - 400. Find the number of pretzels that must be sold to maximize profit.

O A. 359,600 pretzels

OB. 300 pretzels

OC. 600 pretzels

Answer 1

We have been given that the profit that the vendor makes per day by selling x pretzels is given by the function
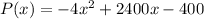`P(x)=-4x^2+2400x-400`. We are asked to find the number of pretzels that must be sold to maximize profit.

First of all, we will find the derivative of our given function.

`P'(x)=-4\cdot 2x^(2-1)+2400`

`P'(x)=-8x+2400`

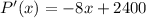
Now, we will find the critical point by equating derivative with 0 as:

`-8x+2400=0`

`-8x+2400-2400=0-2400`

`-8x=-2400`

`(-8x)/(-8)=(-2400)/(-8)`

`x=300`

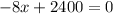
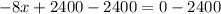
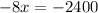
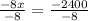
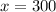
Therefore, the company must sell 300 pretzels to maximize profit and option B is the correct choice.