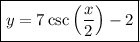Question

The range of a cosecant function is (-infinity, -9}U{5, infinity). The equations of two consecutive asymptotes of the function are x = 0 and x = 2pi. The function is not a reflection over the x-axis. What is the equation of this cosecant function?

Answer 1

`y=7\csc{\left((x)/(2)\right)}-2`

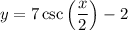
Explanation:

The range of a cosecant function normally excludes the interval (-1, 1). Yours excludes the interval (-9, 5), which has a width 7 times as great. Thus we know the vertical scale factor is 7.

The midpoint of the excluded interval of your function is (-9+5)/2 = -2, so that is the vertical translation.

The cosecant function normally has vertical asymptotes at x=0 and x=π, so your function is expanded horizontally by a factor of 2.

Your cosecant function is ...

`\boxed{y=7\csc{\left((x)/(2)\right)}-2}`