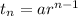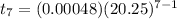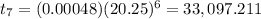Question

The second term of a GP is 4, the fifth term is 81. Find the seventh term

Answer 1

The seventh term of a G.P is

`t_(7) = 33,097.211`

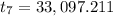
Explanation:

step(i):-

Given the second term of a G.P is '4'

The general term of nth term is

`t_(n) = ar^(n-1)`

`t_(4) = ar^(4-1) =4`

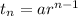
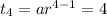
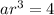`ar^(3) =4` …(i)

Also Given the fifth term of a G.P is '81'

`t_(5) = ar^(5-1) =81`

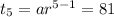
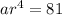`ar^(4) =81` …(ii)

Step(ii):-

Dividing the equation (ii) divided by (i)

`(ar^(4) )/(ar^(3) ) = (81)/(4)`

cancellation ' a' and 'r' terms , we get

`r = (81)/(4)=20.25`

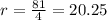
substituting 'r' Value in equation (i), we get

`ar^(3) =4`

`a((81)/(4)) ^(3) =4`

`a = (4X4X4X4)/((81)^(3) )= (256)/(531,441)`

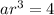
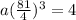
a = 0.00048

Step(iii):-

The seventh term of G.P

The general term of nth term is

`t_(n) = ar^(n-1)`

`t_(7) = (0.00048)(20.25)^(7-1)`

`t_(7) = (0.00048)(20.25)^(6)= 33,097.211`