Question

Solve it
x / 5 + (x - 1) / 3 = 1/5

Answer 1

• x = 1

Explanation:

In the question we have given an equation that is x / 5 + ( x - 1 ) / 3 = 1 / 5 . And we are asking to solve the equation that means we have to find the value of x.

Solution : -

`\longmapsto \qquad (x)/(5) + ((x - 1))/(3) = (1)/(5)`

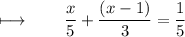
Step 1 : Bye taking L.C.M solving left side :

`\longmapsto \qquad (3x + 5(x - 1))/(15) = (1)/(5)`

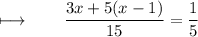
On further calculations, We get :

`\longmapsto \qquad (3x + 5x - 5)/(15) = (1)/(5)`

`\longmapsto \qquad (8x - 5)/(15) = (1)/(5)`

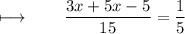
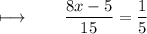
Step 2 : Multiplying 15 on both sides :

`\longmapsto \qquad \frac{8x - 5}{ \cancel{15}} * \cancel{15 } = \frac{1}{ \cancel{5}} * \cancel{15}`

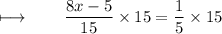
On further calculations, We get :

`\longmapsto \qquad 8x - 5 = 3`

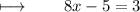
Step 3 : Adding 5 on both sides :

`\longmapsto \qquad8x - \cancel{5} + \cancel{ 5} = 3 + 5`

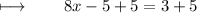
On further calculations, We get :

`\longmapsto \qquad8x = 8`

Step 4 : Dividing with 8 on both sides :

`\longmapsto \qquad \frac{ \cancel{8}x}{ \cancel{8}} = \cancel{(8)/(8) }`

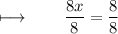
On further calculations, We get :

`\longmapsto \qquad \blue{\underline{\blue{\boxed{ \frak{x = 1}}}}}`

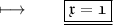
• Henceforth, value of x is 1 .

Verifying : -

We are verifying our answer by substituting value of x in the given equation . So ,

• x / 5 + ( x - 1 ) / 3 = 1 / 5

• 1 / 5 + (1 - 1 ) / 3 = 1 / 5

• 1 / 5 + 0 / 3 = 1 / 5 (0 / 3 is equal to 0)

• 1 / 5 + 0 = 1 / 5

• 1 / 5 = 1 / 5

• L.H.S = R.H.S

• Hence , Verified .

Therefore, our solution is correct .

#Keep Learning