Question

At 517 mm Hg and 24 °C, a sample of gas occuples a volume of 95 ml. The gas is transferred to a 225-ml flask and the temperature is reduced to -

8.0 °C. What is the pressure of the gas in the flask in mmHg?

Answer 1

195mmHg is the pressure of the flask

Step-by-step explanation:

Combined gas law defines the relationship of pressure, absolute temperature and volume of a gas under different conditions. The formula is:

`(P_1V_1)/(T_1) =(P_2V_2)/(T_2)`

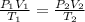
In the problem, initial conditions of the gas are:

517mmHg = P₁

24°C + 273.15 = 297.15K = T₁

95mL = V₁

And final conditions are:

225mL = V₂

8.0°C + 273.15 = 265.15K = T₂

Replacing:

`(517mmHg*95mL)/(297.15K) =(P_2*225mL)/(265.15K)`

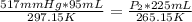
P₂ = 195mmHg is the pressure of the flask

Answer 2

`P_2=194.78mmHg`

Step-by-step explanation:

Hello,

In this case, we employ the combined ideal gas law in order to understand the volume-gas-pressure behavior as shown below:

`(P_1V_1)/(T_1)= (P_2V_2)/(T_2)`

Hence, solving for the final pressure P2, we obtain (do not forget temperature must be absolute):

`P_2=(P_1V_1T_2)/(V_2T_1)=(517mmHg*95mL*(-8.0+273.15)K)/((24+273.15)K*225mL)\\ \\P_2=194.78mmHg`

Best regards.