Answer:
1). m∠ACB = 20°
2). central angle measure = 156°
inscribed angle measure = 78°
circumscribed angle measure = 24°
Explanation:
1). Measure of ∠AOB = 40°.
Since m∠ACB =
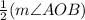
m∠ACB =
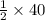
= 20°
2). Measure of the central angle of the the given circle, m ∠BOD = 156°
Inscribed angle, m∠BAD =
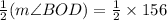
= 78°
Circumscribed angle m∠BCD =
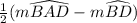
=
![(1)/(2)[(360-156)-156]](https://img.qammunity.org/2021/formulas/mathematics/college/yixtogx7gepk04djmecd742im2ewmukekb.png)
=
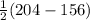
=
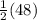
= 24°
Therefore, central angle measure = 156°
inscribed angle measure = 78°
circumscribed angle measure = 24°