Please consider the diagram.
We have been given that the volume of the triangular prism is 54 cubic units. We are asked to find the value of x.
We know that volume of triangular prism is equal to area of base times height of the prism.
We can see from the attachment that base of prism is triangle. The area of the base of prism would be equal to area of triangle.
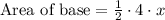
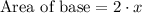
Now we will multiply base area with height of prism
 .
.
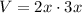
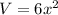
Let us equate volume of prism with 54 as:
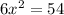
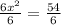
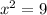
Take positive square root on both sides:
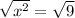
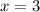
Therefore, the value of x is 3 and option A is the correct choice.