Question

In ΔFGH, the measure of ∠H=90°, GF = 53, HG = 28, and FH = 45. What ratio represents the sine of ∠G?

Answer 1

The sine of angle G in triangle FGH is approximately 0.5283.

Step-by-step explanation:

In triangle FGH, we are given that angle H is 90 degrees, GF is 53, HG is 28, and FH is 45. To find the ratio that represents the sine of angle G, we need to use the definition of sine. Sine is the ratio of the length of the side opposite the angle to the length of the hypotenuse. In this case, HG is opposite angle G and FG is the hypotenuse. Therefore, the sine of angle G is given by sin(G) = HG/FG.

Substituting the given values, sin(G) = 28/53 ≈ 0.5283.

Answer 2

we have been given that in ΔFGH, the measure of ∠H=90°, GF = 53, HG = 28, and FH = 45. We are asked to find the ratio that represents the sine of ∠G.

First of all, we will draw a right triangle using our given information.

We know that sine relates opposite side of right triangle with hypotenuse.

`\text{sin}=\frac{\text{Opposite}}{\text{hypotenuse}}`

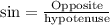
We can see from the attachment that opposite side to angle G is FH and hypotenuse is GF.

`\text{sin}(\angle G)=(FH)/(GF)`

`\text{sin}(\angle G)=(45)/(53)`

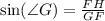
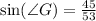
Therefore, the ratio
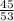`(45)/(53)` represents the sine of ∠G.