Question

If a=√2+1,find the value of (a-1/a)²

Answer 1

Answer is in the picture

Hope this helps ^-^

Answer 2

Explanation:

Let us assume that we are asked to find the value of:

[ (a − 1) / a] ² ;

Given: " a = √2 + 1 " ;

Substitute this value for "a" into the given expression.

Start with " (a − 1) " ;

→ " √2 + 1 − 1 = √2 " .

_______________________

Then, the denominator is: "a" ; so we plug in: "√2 + 1 " ; for "a" ;

→ [ (a − 1) / a] ² ;

= {√2 / (√2 -1)]²

=
`((√(2) )/((√(2)-1)))^(2)` ;

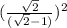Note: Start with the "numerator" :

"
`(√(2) *√(2)) =2` . "

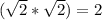Then, continue with the "denominator":

"
`(√(2) -1)^(2) = (√(2)-1)(√(2)-1)`
`= ?` " ;

_______________________________________

`(√(2) -1)^(2) = (√(2)-1)(√(2)-1)` ;

________________________________________

→
`(√(2)-1)(√(2)-1) = ?`

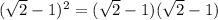
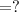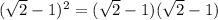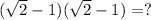
→ Use the "FOIL" method (First, Outer, Inner, and Last terms, in that Order; then, combine the "like forms" to simply:

First terms: √2*√2 = + 2 ;

Outer terms: √2* -1 = -1√2 ;

Inner terms: -1 * √2 = -1√2 ;

Last terms: -1 * -1 = +1 ;

______________________________

Now, write these terms down in order:

+2 -1√2 - 1√2 + 1 ;

Now, combine the "like terms:

-1√2 - 1√2 = - 2√2 ;

_____________

+ 2 + 1 = 3 .

So; we have: - 2√2 + 3 ; for the denominator.

The answer is: 2/ (-2√3 + 3) ;

or, write as: 2/ (3 - 2√3).

So, the answer is: 2 /