Question

Three charges of magnitude 3.0\times 10^{-4}3.0 × 10 − 4 C each are located at x = 1.0 m, y = Three charges of magnitude 3.0\times 10^{-4}3.0 × 10 − 4 C each are located at x = 1.0 m, y = 0.0 m, at x = 0.0 m, y = 0.0 m, and at x = -1.0 m, y = 0.0 m. The one in the middle is negative, while the other two are positive.

What is the net Coulombic force exerted by them on a negative \times10^{-5}3.0 × 10 − 5 C charge located at x = 0.0 m, y = 2.0 m(the value of k is 9.0x10^9 N.m^2/C^2)

Answer 1

The negative charge at x = 0.0 m, y = 2.0 m experiences a net Coulombic force of 5.49 N upwards, calculated using Coulomb's Law considering the forces exerted by the surrounding charges.

Step-by-step explanation:

Calculation of Net Coulombic Force

To calculate the net Coulombic force acting on the negative charge located at x = 0.0 m, y = 2.0 m, we need to apply Coulomb's Law. This law states that the force between two point charges is proportional to the product of their charges and inversely proportional to the square distance between them, with the equation F = (k * |q_1 * q_2|) / r^2, where k is Coulomb's constant.

Let's denote the three charges as Q1, Q2, and Q3, and the test charge as q. Charge Q1 (+3.0 x 10^-4 C) is located at x = 1.0 m, Q2 (-3.0 x 10^-4 C) at x = 0.0 m, and Q3 (+3.0 x 10^-4 C) at x = -1.0 m. The test charge q (-3.0 x 10^-5 C) is at x = 0.0 m, y = 2.0 m. By symmetry, the horizontal components of the forces exerted by charges Q1 and Q3 on the test charge cancel each other out, so we only need to calculate the vertical components.

The distance r from Q1 or Q3 to q is √((1.0)^2 + (2.0)^2) = √5 m. Using Coulomb's Law, the force by each charge is:
F = (9.0 x 10^9 N.m^2/C^2 * 3.0 x 10^-4 C * 3.0 x 10^-5 C) / (√5)^2 = (9.0 x 10^9 * 9.0 x 10^-9 N) / 5 = 1.62 N.

The force exerted by Q2 (vertical) on q is:
F = (9.0 x 10^9 N.m^2/C^2 * (-3.0 x 10^-4 C) * (-3.0 x 10^-5 C)) / (2.0)^2 = (9.0 x 10^1 N) / 4 = 2.25 N upwards.

Therefore, the net Coulombic force on q will be the vector sum of these individual forces: 2 * 1.62 N (from Q1 and Q3) upwards plus 2.25 N upwards from Q2, giving a total of 5.49 N upwards.

Answer 2

F = 8.98 j N

Step-by-step explanation:

Coulomb's strength is given by

`F_(e)` = k q₁ q₂ / r₁₂²

this force applied between each pair of electric charges and the total force is the sum of all the forces

F = F₁₄ + F₂₄ + F₃₄

where charge 1 is at position x = 1.0, charge 2 at x = 0 and charge 3 at x = -1.0 m, the cahrge 4 at point x = 0 y = 2.0 m

The force between charge 2 and 4 is attractive because of different signs

F₂₄ = k q₂q₄ / r₂₄²

r₂₄ = 0-2

F₂₄ = 9 10⁹ 3 10⁻⁴ 3 10⁻⁵ / 2²

F₂₄ = 20 N in y axis

The force between charges 1 and 4 is

F₁₄ = k q₁ q₄ / r₁₄²

r₁₄² = (1-0)² + (0-2)²

r₁₄² = 5

F₁₄ = 9 10⁹ 3 10⁻⁴ 3 10⁻⁵ / 5

F₁₄ = 16.2 N

this force is repulsive since the two charges have the same sign.

Let's use trigonometry to find its components

tan θ = y / x

θ = tan⁻¹ 2/1

θ = 63.4º

let's break down the force

sin 63.4 =
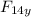`F_(14y)` / F

cos 63.4 = F_{14x} / F

F_{14y} = F sin 63.4 = 16.2 sin 63.4

F_{14y} = 14.49 N

F_{14x} = F cos 63.4 = 16.2 cos 63.4

F_{14x} = -15.69 N

The force between charges 3 and 4 has the same magnitude and angles, so its value is

F₃₄ = 16.2 N

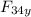`F_(34y)` = 14.49 N

F_{34x} = 15.69 N

to find the total force we add each component

Fₓ = F_{14x} + F_{24x} + F_{34x}

Fₓ = -15.69 + 0 + 15.69

Fₓ = 0

F_{y} = F_{14y} + F_{24y} + F_{34y}

F_{y} = 14.49 - 20 + 14.49

F_{y} = 8.98 N

the total force is

F = 8.98 j N