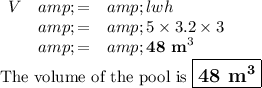Answer:
Explanation:
Q1.
a) Width of field
The formula for the area of a rectangle is
A = lw
Data
A = 800 a
l = 0.8 km
Calculations
(i) Convert all measurements to metres
A = 800 a × 100 m²/a = 80 000 m²
l = 0.8 km × 1000 m/1 km = 800 m
(ii) Calculate the width
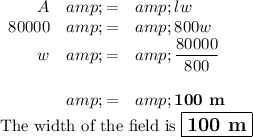
b) Perimeter of field
The formula for the perimeter of a rectangle is

Q2.
a) Number of tiles
Data:
l = 5 m
w = 32 dm
h = 3 m
Tile edge = 20 cm
(i) Convert all measurements to metres
w = 32 dm × (1 m/10 dm) = 3.2 m
Tile edge = 20 cm × (1 m/100 cm) = 0.20 m
(ii) Area of pool bottom
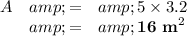
(iii) Area of one tile
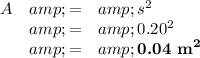
(iv) Number of tiles
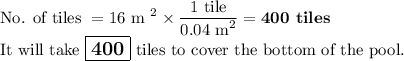
b) Volume of pool
The formula for the volume of a rectangular prism is\begin{array}{rcl}