Question

Trevor is analyzing a circle, y2 + x2 = 100, and a linear function g(x). Will they intersect? y2 + x2 = 100 g(x) graph of the function y squared plus x squared equals 100 x g(x) −1 −22 0 −20 1 −18

Yes, at positive x coordinates
Yes, at negative x coordinates
Yes, at negative and positive x coordinates
No, they will not intersect

Answer 1

Yes, at positive x coordinates

Explanation:

Find the equation of g(x)

Given ordered pairs of g(x): (-1, -22) (0, -20) (1, -18)

`\sf let\:(x_1,y_1)=(0,-20)`

`\sf let\:(x_2,y_2)=(1,-18)`

`\sf slope\:(m)=(y_2-y_1)/(x_2-x_1)=(-18-(-20))/(1-0)=2`

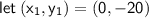
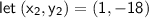
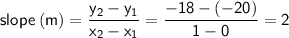
Point-slope form of linear function:
`\sf y-y_1=m(x-x_1)`

`\implies \sf y-(-20)=2(x-0)`

`\implies \sf y=2x-20`

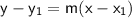
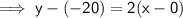
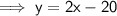
Substitute the equation of g(x) into the equation of the circle and solve for x

Given equation:
`y^2+x^2=100`

`\implies (2x-20)^2+x^2=100`

`\implies 4x^2-80x+400+x^2=100`

`\implies 5x^2-80x+300=0`

`\implies x^2-16x+60=0`

`\implies x^2-10x-6x+60=0`

`\implies x(x-10)-6(x-10)=0`

`\implies (x-6)(x-10)=0`

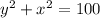
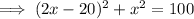
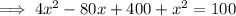
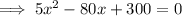
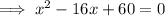
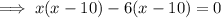
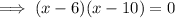
Therefore:

`(x-6)=0 \implies x=6`

`(x-10)=0 \implies x=10`

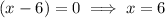
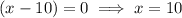
So the linear function g(x) will intersect the equation of the circle at positive x coordinates.