Question

Jimmy invests $17,000 in an account that pays 4.70% compounded quarterly. How long (in years and months) will it take for his investment to reach $22,000?

Answer 1

We have been given that Jimmy invests $17,000 in an account that pays 4.70% compounded quarterly. We are asked to find the time it will take for Jimmy's investment to reach $22,000.

We will use compound interest formula to solve our given problem.

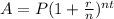`A=P(1+(r)/(n))^(nt)`, where,

A = Amount after t years,

P = Principal amount,

r = Annual interest rate in decimal form,

n = Number of times interest is compounded per year,

t = Time in years.

`P = 17,000`,
`A=22,000`,
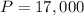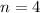`n=4` and
`r=(4.70)/(100)=0.047`.

`22,000=17,000(1+(0.047)/(4))^(4\cdot t)`

`22,000=17,000(1+0.01175)^(4\cdot t)`

`22,000=17,000(1.01175)^(4\cdot t)`

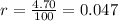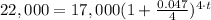
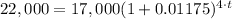
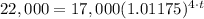
Switch sides:

`17,000(1.01175)^(4\cdot t)=22,000`

`(17,000(1.01175)^(4\cdot t))/(17,000)=(22,000)/(17,000)`

`(1.01175)^(4\cdot t)=(22)/(17)`

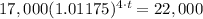
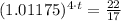
Now we will take natural log on both sides:

`\text{ln}((1.01175)^(4\cdot t))=\text{ln}((22)/(17))`

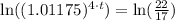
Applying rule
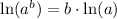`\text{ln}(a^b)=b\cdot\text{ln}(a)`, we will get:

`4t\cdot\text{ln}(1.01175)=\text{ln}((22)/(17))`

`t=\frac{\text{ln}((22)/(17))}{4\text{ln}(1.01175)}`

`t=(0.2578291093020998)/(4\cdot 0.0116815047738379)`

`t=(0.2578291093020998)/(0.0467260190953516)`

`t=5.517891622`

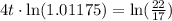
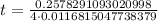
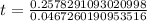
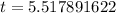
0.52 years will be approximately 6 months.

Therefore, it will take 5 years and 6 months to reach Jimmy's investment to reach $22,000.