Answer:
t-shirts: 2790
profit: $12209
Explanation:
Given the function:
p(x) = -x³ + 4x² + x
we want to maximize it.
The following criteria must be satisfied at the maximum:
dp/dx = 0
d²p/dx² < 0
dp/dx = -3x² + 8x + 1 = 0
Using quadratic formula:
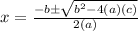
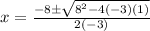
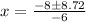
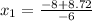

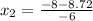
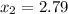
d²p/dx² = -6x + 8
d²p/dx² at x = -0.12: -6(-0.12) + 8 = 8.72 > 0
d²p/dx² at x = 2.79: -6(2.79) + 8 = -8.74 < 0
Then, he should prints 2.79 thousands, that is, 2790 t-shirts to make maximum profits.
Replacing into profit equation:
p(x) = -(2.79)³ + 4(2.79)² + 2.79 = 12.209
that is, $12209