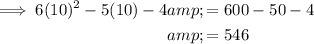Answer:
(a) when x = 2: width = 2 units and length = 5 units
(b) 546 units²
Explanation:
Given expression:
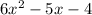
Part (a)
To factor a quadratic in the form
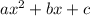
Find 2 two numbers that multiply to
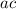 and sum to
and sum to
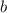
Two numbers that multiply to -24 and sum to -5: -8 and 3
Rewrite
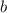 as the sum of these 2 numbers:
as the sum of these 2 numbers:
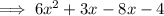
Factorize the first two terms and the last two terms separately:
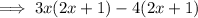
Factor out the common term
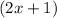 :
:
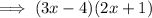
Therefore:
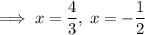
As distance is positive,
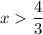
Let
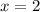
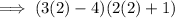
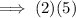
Therefore, possible dimensions of the rectangle are:
width = 2 units
length = 5 units
Part (b)
Substitute
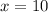 into the equation:
into the equation: