PLEASE HELP NEED THIS DONE ASAP Find the area of rhombus PQRS. Round to the nearest tenth if necessary. (Hint, use pythagorean theorem to find a missing side of the diagonal).

Question

asked Mar 8, 2021 196k views

1 Answer

Abhinav Ramakrishnan · Answer 1 · 2021-03-11T18:05:06+0000

Answer:

The area of rhombus PQRS is 120 m.

Explanation:

Consider the rhombus PQRS.

All the sides of a rhombus are equal.

Hence, PQ = QR = RS = SP = 13 m

The diagonals PR and QS bisect each other.

Let the point at of intersection of the two diagonals be denoted by X.

Consider the triangle QXR.

QR = 13 m

XR = 12 m

The triangle QXR is a right angled triangle.

Using the Pythagorean theorem compute the length of QX as follows:

QR² = XR² + QX²

QX² = QR² - XR²

= 13² - 12²

= 25

QX = √25

= 5 m

The measure of the two diagonals are:

PR = 2 × XR = 2 × 12 = 24 m

QS = 2 × QX = 2 × 5 = 10 m

The area of a rhombus is:

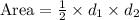
$\text{Area}=(1)/(2)* d_(1)* d_(2)$

Compute the area of rhombus PQRS as follows:

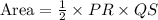
$\text{Area}=(1)/(2)* PR* QS$

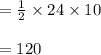
$=(1)/(2)* 24* 10\\\\=120$

Thus, the area of rhombus PQRS is 120 m.