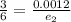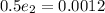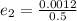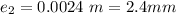Question

3. A certain wire, 3 m long, stretches by 1.2 mm when under tension of 200 N. By how much does

an equally thick wire 6 m long, made of the same material and under the same tension, stretch?
​

Answer 1

The extension of the second wire is
`e_2 = 0.0024 \ m = 2.4 mm`

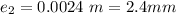
Step-by-step explanation:

From the question we are told that

The length of the wire is
`L = 3 \ m`

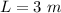
The elongation of the wire is
`e = 1.2mm = (1.2)/(1000) = 0.0012 m`

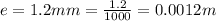
The tension is
`F = 200 \ N`

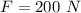
The length of the second wire is
`L_2 = 6 \ m`

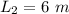
Generally the Young's modulus(Y) of this material is

`Y = (stress)/(strain )`

Where
`stress = (F)/(A)`

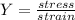
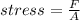
Where A is the area which is evaluated as

`A = \pi r^2`

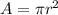
and
`strain = (extention)/(length) = (e)/(L)`

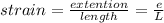
So

`Y = ((F)/(\pi r^2 ) )/( (e)/(L) )`

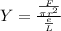
Since the wire are of the same material Young's modulus(Y) is constant

So we have

`(F * L )/(r^2 e) = \pi * Y = constant`

`F * L = constant * r^2 e`

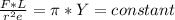
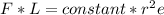
Now the ration between the first and the second wire is

`(F_1)/(F_2) * (L_1)/(L_2) = (r*2_1)/(r^2) * (e_1)/(e_2)`

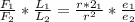
Since tension , radius are constant

We have

`(L_1)/(L_2) = (e_1)/(e_2)`

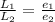
substituting values

`(3)/(6) = (0.0012)/(e_2)`

`0.5 e_2 = 0.0012`

`e_2 = ( 0.0012 )/(0.5)`

`e_2 = 0.0024 \ m = 2.4 mm`